Yes Please Proceed
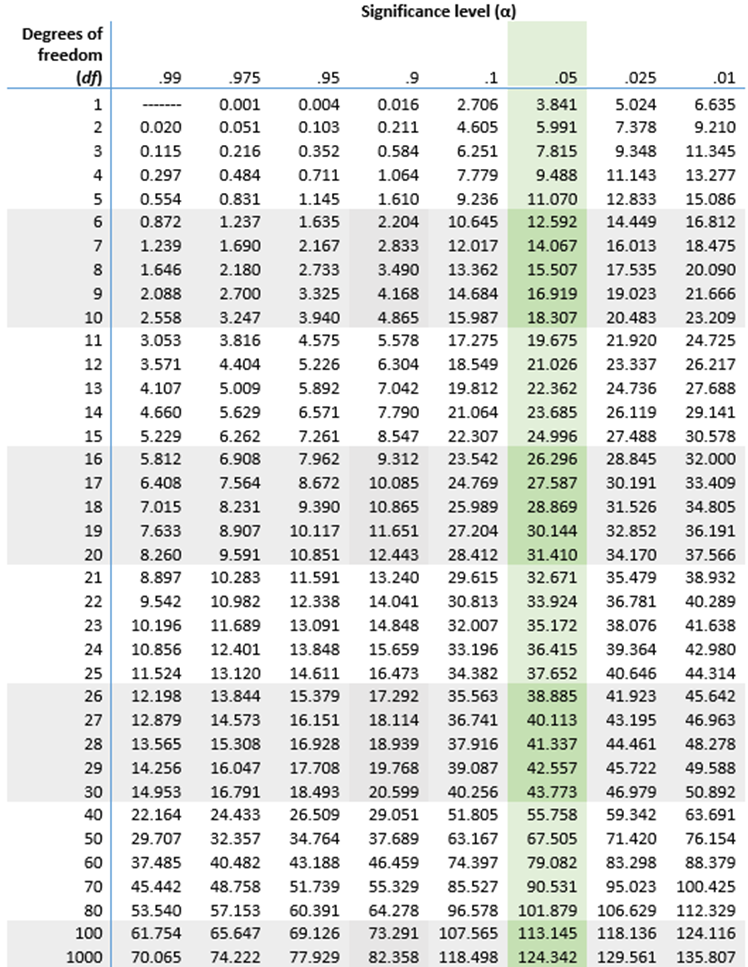
The Chi-Square distribution table provides critical values for a given probability level and degrees of freedom. These critical values, denoted by χ^2, are used to determine the likelihood of a chi-square test result being due to chance. The table lists critical values for different probability levels such as .995, .99, .975, .95, .9, .1, .05, .025, and .01, with corresponding degrees of freedom.
First, we need to calculate the test statistic. This is given by the formula:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
Where:
- ( O_i ) = Observed frequency for the ( i^{th} ) category
- ( E_i ) = Expected frequency for the ( i^{th} ) category
Using the observed (( O_i )) and expected (( E_i )) frequencies provided earlier, we'll calculate the test statistic using the formula.
Next, we'll use the test statistic with the chi-square distribution table to find the p-value. The p-value is the probability of observing a test statistic as extreme as, or more extreme than, the one actually observed, assuming that the null hypothesis is true. We'll locate the p-value associated with the calculated test statistic and the degrees of freedom (which is 4 - 1 = 3).
Let me calculate the test statistic and p-value using the given observed and expected frequencies.
Sources

Related Questions
Work fast from anywhere
Stay up to date and move work forward with BrutusAI on macOS/iOS/web & android. Download the app today.
