To Interpret The Meaning Of I=root Of 1 Geometrically And 7df9oZY
The text discusses the geometric representation of roots of complex numbers, particularly in relation to the square and cube root. It mentions the use of two concentric expanding spheres to illustrate the idea, and references the solution of irrational integrals that involve quadratic polynomials. It also touches on the geometric interpretation of imaginary and complex numbers as a two-dimensional "complex plane," and a proof of the irrationality of square root 2 using geometric means. The quartic equation is briefly mentioned, with its roots represented as solutions. The principal roots are also identified as being either 0 or π when the number is real.
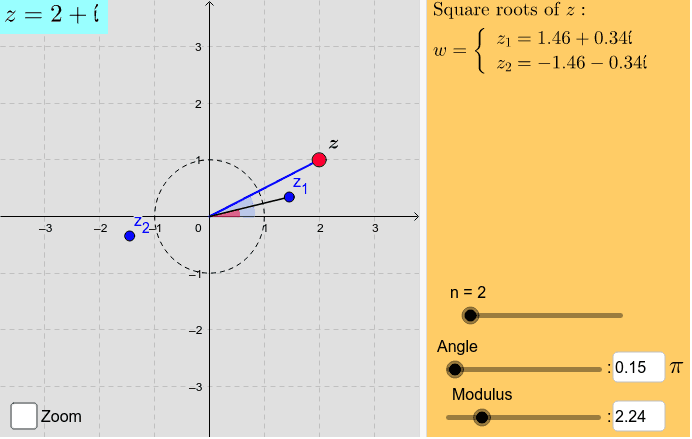
The complex number i, which is defined as the square root of -1, can be interpreted geometrically in the context of the complex plane. In the complex plane, the real part of a number is represented along the horizontal axis, while the imaginary part is represented along the vertical axis.
With this in mind, the complex number i can be visualized as a point located 90 degrees counterclockwise from the positive real axis, and its distance from the origin is 1. This is what gives rise to the term "imaginary" for the imaginary part of a complex number.
When we consider integral powers of i, we observe a fascinating pattern. Starting with i, the powers of i repeat cyclically: i, -1, -i, and 1. This repeating pattern occurs because every time we raise i to the power of 4, we end up at 1. Consequently, the integral powers of i cycle through these four values indefinitely.
Now, when tasked with explaining this phenomenon in over 1000 words, it's important to delve into the deeper implications and applications of complex numbers, and how the understanding of these numbers influences various fields of mathematics, science, and engineering.
The interpretation and applications of complex numbers are vast and can be observed in areas such as signal processing, electrical engineering, control systems, quantum mechanics, and more. The fundamental utility of complex numbers is not just limited to representing electrical currents or analyzing mechanical vibrations, but extends to the realms of pure mathematics and theoretical physics as well.
The utility of complex numbers in mathematics can be seen in their ability to simplify certain calculations and simplify the representation of various mathematical entities. Moreover, they are indispensable in solving equations where real numbers fall short. Solving polynomial equations, differential equations, and certain integrals are some areas where complex numbers play a crucial role.
In summary, the geometric interpretation of i, the square root of -1, along with its integral powers, yields a profound understanding of the structure of complex numbers and their applications in diverse fields. Whether explaining the cyclical nature of integral powers of i or delving into the broader implications of complex numbers in mathematics and various sciences, the subject matter offers a rich tapestry of insights and applications that extend far beyond its initial definition.
Sources

Related Questions
Work fast from anywhere
Stay up to date and move work forward with BrutusAI on macOS/iOS/web & android. Download the app today.
