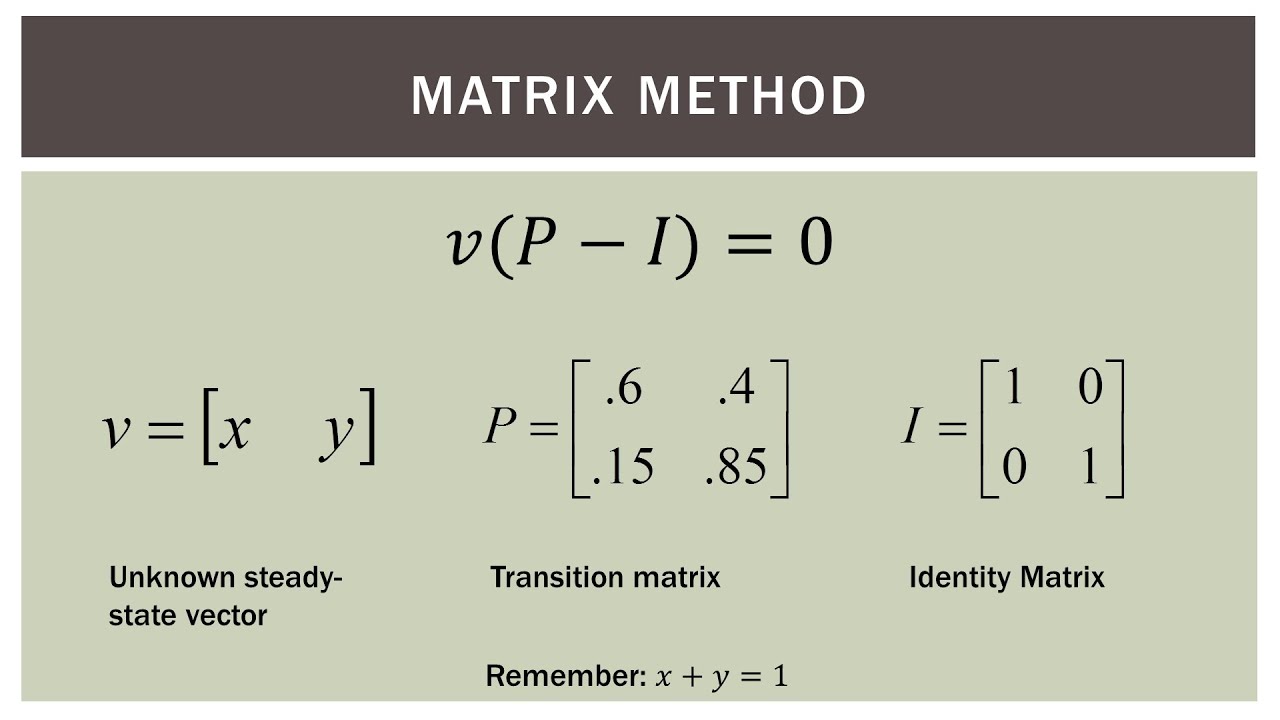The Probability That An Assembly Line Works Correctly Depends On 7ejQpuJ
The text discusses the features and capabilities of a Markov chain calculator, specifically its ability to calculate probabilities for a given number of steps, steady state vector, and absorbing states. It also mentions the input required for the calculator and its use in a finite Markov chain process. Additionally, the author mentions a fix made to a markovchain package in August 2016 and the use of a function in R to calculate eigen vectors and values. The calculator is also mentioned in the context of finding steady state probabilities in three different examples. The post ends with instructions and an example of using the calculator to find the chances of a "chance driver" choosing a specific option.
To find the probability that the assembly line will work in the long run, we can use the concept of a Markov chain. In this case, the probabilities of the assembly line working correctly depend on the previous state.
The long-run behavior of a Markov chain can be determined by finding the steady state probabilities. These probabilities represent the probabilities of the system being in each state in the long run.
To calculate the steady state probabilities for the given transition matrix, specialized tools are typically used, such as a Markov Chain steady state calculator. These tools can provide the steady state probabilities for the given transition probabilities.
If you have the specific transition probabilities for the assembly line, you can input them into a Markov Chain steady state calculator to obtain the probability that the line will work in the long run.
Work fast from anywhere
Stay up to date and move work forward with BrutusAI on macOS/iOS/web & android. Download the app today.