The limits of the arc cotangent function, or arccot(x), can be explored through several resources that provide insight into its behavior and properties.

1. Evaluate the Limit as x Approaches 0: According to Mathway, as x approaches 0, the limit of arccot(x) evaluates to π/2. This result indicates the behavior of the function near the origin, illustrating that arccot(0) essentially corresponds to a π/2 angle. You can learn more about this specific limit here.

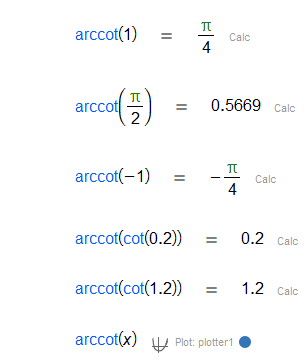
2. Inverse Cotangent Properties: The website Mathwords states that the range for the inverse cotangent function, often represented as cot^(-1), is typically restricted to the interval (0, π). This is important when considering the output values of the arccot function, as it assures that the limits will fall within this range. For further information on this, you can visit Mathwords.

3. General Considerations in Trigonometric Limits: The Mathematics LibreTexts site discusses various limits of trigonometric functions, including mention of key limits involving inverse trig functions like arccot. Specifically, as x approaches ±∞ for related functions, understanding these can help consolidate your grasp of trigonometric limits. More details can be found here.

4. Graphing and Interpretation: In discussions about the graph of arccot, Intmath elaborates that the correct range is indeed from 0 to π, reinforcing the earlier note about cotangent inverse properties and its graphical representation. You can read more about this graphing aspect here.

5. Derivation and Insights: Edulyte provides a deeper look into the definition and implications of the arccotangent function, including how it represents angles whose cotangent matches a given number. This foundational perspective can enhance understanding before diving into limits. For more insights, check Edulyte.

6. Continuity and Limits of Inverse Trigonometric Functions: Finally, Mathematics LibreTexts also covers limits and continuity specific to inverse trigonometric functions, including arccot and its behaviors at extreme values, enriching overall understanding. The details can be explored here.

These resources collectively provide substantial information on the limits of the arc cotangent function and its characteristics, aiding anyone interested in delving deeper into the topic.

Sources

Evaluate the Limit limit as x approaches 0 of arccot(x) - MathwayInverse Cotangent - Mathwords1.7: Limit of Trigonometric functions - Mathematics LibreTextsarccot limit: $\sum_{r=1}^{\infty}\cot ^{-1}(r^2+\frac{3}{4})Which is the correct graph of arccot x? - Interactive MathematicsDemystifying the Arccot Formula: Trigonometric Insights - Edulyte1.8: Limits and continuity of Inverse Trigonometric functions

Related Questions

What is the range of Arccotx?

Why is arccos range 0 to pi?

How to calculate arcctg?