Forty Randomly Selected Students Were Asked The Number Of Pairs
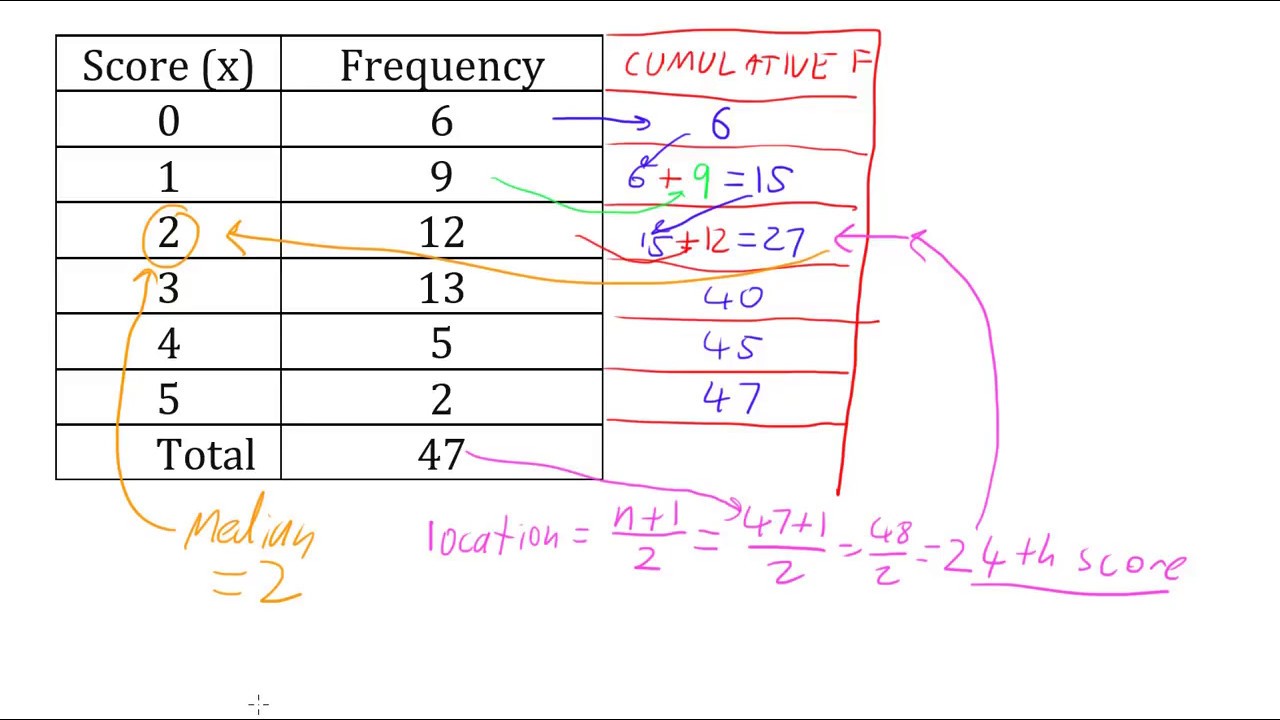
The median is a statistical measure of central tendency that represents the middle value of a set of data. It can be calculated by finding the midpoint or average of the two middle values, and it is often used to understand numerical trends in a set of data. Cumulative frequency can also be used to determine the median, and it is essential to use a cumulative frequency distribution to find the midpoint value. In a frequency distribution, the median is the value at which half of the observations lie above and half lie below. This measure is useful in understanding the central tendency of a set of data and is commonly used in statistical analysis.
To find the median for the given frequency distribution, we can follow these steps:
- Arrange the data in ascending order.
- Calculate the cumulative frequency.
- Identify the median class, which contains the median.
- Use the formula to calculate the median as:
[ \text{Median} = L + \left( \frac{\frac{n}{2} - F}{f} \right) \times c ]
where:
- ( L ) = Lower class boundary of the median class
- ( n ) = Total frequency
- ( F ) = Cumulative frequency of the class before the median class
- ( f ) = Frequency of the median class
- ( c ) = Class width
Let me perform the necessary calculations for you.
Sources

Related Questions
Work fast from anywhere
Stay up to date and move work forward with BrutusAI on macOS/iOS/web & android. Download the app today.
