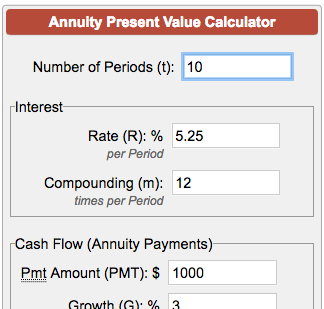
compute the PV of annuity using the following information and
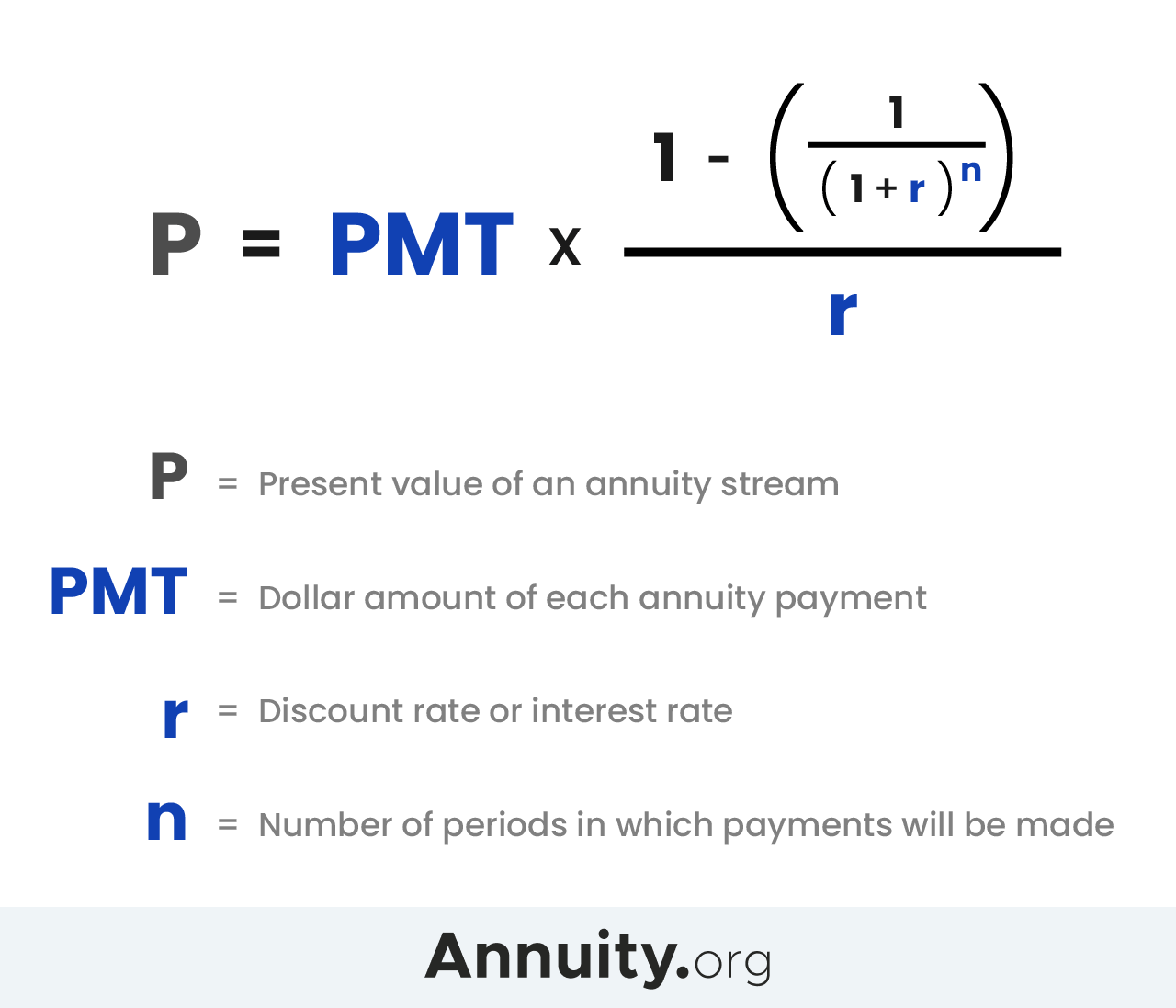
To calculate the present value (PV) of an annuity with the given information—an APR of 6%, monthly payments of $500, and a duration of 5 years—we can use the formula for the present value of an annuity:
[ PV = P \times \left( \frac{1 - (1 + r)^{-n}}{r} \right) ]
Where:
- (P) = monthly payment = $500
- (r) = monthly interest rate = ( \frac{0.06}{12} = 0.005)
- (n) = total number of payments = (5 \times 12 = 60)
Step-by-step Calculation:
-
Calculate ( (1 + r)^{-n} ): [ (1 + 0.005)^{-60} \approx (1.005)^{-60} \approx 0.740818 ]
-
Calculate ( 1 - (1 + r)^{-n} ): [ 1 - 0.740818 \approx 0.259182 ]
-
Compute the fraction: [ \frac{0.259182}{0.005} \approx 51.8364 ]
-
Finally, compute the present value: [ PV = 500 \times 51.8364 \approx 25918.20 ]
Result:
The present value of the annuity is approximately $25,918.20.
If you'd like to confirm this calculation using online tools, here are some useful links:
- Financial Mentor's Present Value of Annuity Calculator
- Calculator Soup's Present Value of Annuity Calculator
- Omni Calculator's Present Value of Annuity Calculator
Feel free to reach out if you have any further questions!
Work fast from anywhere
Stay up to date and move work forward with BrutusAI on macOS/iOS/web & android. Download the app today.